Comment distinguer une raquette de tennis d’un stylo à bille

L’article a notamment été sélectionné comme une suggestion de l’éditeur.
Si on lance une raquette et un stylo en l’air, ils n’effectuent pas le même mouvement de rotation. Pourquoi ?
Plus connu sous le nom d’« effet Djanibekov », il décrit ce qui se produit pour tout corps rigide en impesanteur (ou chute libre) qui présente trois axes principaux d’inerties différentes et qui est mis en rotation autour de l’axe d’inertie.
L’exemple de la raquette de tennis :
Si on essaie de faire pivoter la raquette dans les airs sur son axe transversal, on observe un phénomène plutôt surprenant : en plus d’une rotation de 360° autour de l’axe transversal, la raquette effectue presque systématiquement une rotation supplémentaire de 180° autour de son axe longitudinal. Lorsqu’on rattrape la raquette, sa face inférieure est désormais tournée vers le haut.
L’expérience diffère selon l’objet lancé dans les airs. En effet, après une rotation complète du stylo à bille, l’attache est toujours orientée vers la gauche, ce qui signi?fie que le stylo n’a pas eff?ectué le même mouvement que la raquette de tennis : « l’attache permet alors de briser la symétrie du stylo et de dé?finir sans ambiguïté sa position.»
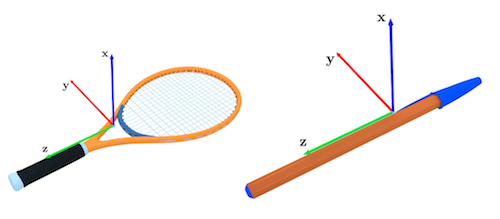
Figure 1 – Définition des axes d’inertie principaux pour une raquette de tennis et un stylo bille.
Pourquoi étudier cette propriété ?
Ce célèbre effet, rarement abordé dans les livres de physique courants, est pourtant un des plus vieux sujets de mécanique classique. C’est par cette motivation que Dominique Sugny et son équipe ont choisi de répondre à ce problème en proposant une formule mathématique ainsi que de nouvelles applications permettant de prévoir à partir de trois paramètres seulement les objets pour lesquels cet effet se manifeste.
- Voir l’article complet : Geometric origin of the Tennis Racket Effect, P. Mardesic, G. J. Gutierrez Guillen, L. Van Damme and D. Sugny, Phys. Rev. Lett. 125, 064301 (2020)
- Revue : Images des mathématiques
- Culture scientifique, technique et industrielle
- Physical Review Letters
- kc_data:
- a:8:{i:0;s:0:"";s:4:"mode";s:2:"kc";s:3:"css";s:0:"";s:9:"max_width";s:0:"";s:7:"classes";s:0:"";s:9:"thumbnail";s:0:"";s:9:"collapsed";s:0:"";s:9:"optimized";s:0:"";}
- kc_raw_content:
